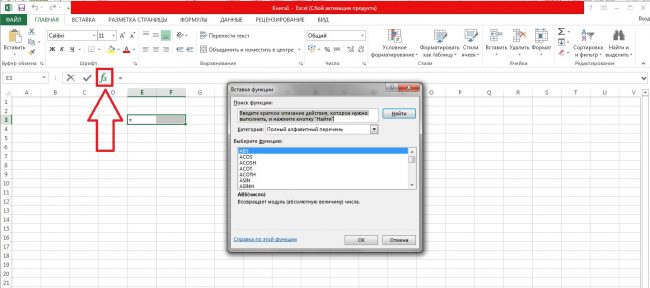
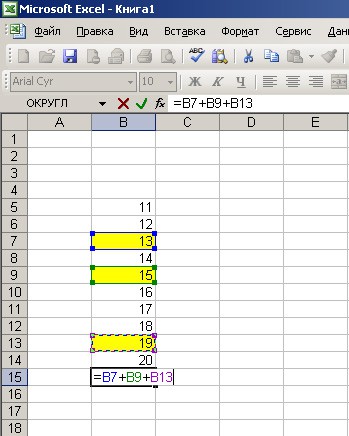
Построение графиков в microsoft excel

Что дает HTTPS для ранжирования сайта?

Как сделать чертеж в Word

Программа Компас-3D — это система автоматизированного проектирования (САПР), предоставляющая широкие возможности по созданию и оформлению конструкторской и проектной документации. Создан данный продукт отечественными разработчиками, отчего он особенно популярен в странах СНГ.

Компас 3D — программа для черчения

Не менее популярным, причем, по всему миру, является и текстовый редактор Word, созданный компанией Microsoft. В этой небольшой статье мы рассмотрим тему, которая касается обеих программ. Как вставить фрагмент из Компаса в Ворд? Этим вопросом задаются многие пользователи, часто работающие в обеих программах, и в этой статье мы дадим на него ответ.

Урок: Как вставить таблицу Word в презентацию

Забегая вперед, скажем, что в Ворд можно вставлять не только фрагменты, но и чертежи, модели, детали, созданные в системе Компас-3D. Сделать все это можно тремя разными способами, о каждом из них мы и расскажем ниже, двигаясь от простого к сложному.

Урок: Как пользоваться Компасом-3D

Вставка объекта без возможности дальнейшего редактирования

Самый простой метод вставки объекта — это создание его скриншота и последующее добавление в Word в виде обычного изображения (рисунка), непригодного для редактирования, как объект из Компаса.

1. Сделайте скриншот окна с объектом в Компасе-3D. Для этого выполните одно из нижеуказанных действий:

• нажмите клавишу «PrintScreen» на клавиатуре, откройте какой-нибудь графический редактор (например, Paint) и вставьте в него изображение из буфера обмена (CTRL+V). Сохраните файл в удобном для вас формате;
• используйте программу для создания скриншотов (например, «Скриншоты на Яндекс Диске»). Если у вас на компьютере не установлено такой программы, выбрать подходящую вам поможет наша статья.

Программы для создания скриншотов

2. Откройте Ворд, кликните в том месте, куда нужно вставить объект из Компаса в виде сохраненного скриншота.

3. Во вкладке «Вставка» нажмите кнопку «Рисунки» и выберите с помощью окна проводника сохраненный вами снимок.

Урок: Как в Word вставить рисунок

Вставка объекта в виде рисунка

Компас-3D позволяет сохранять создаваемые в нем фрагменты в виде графических файлов. Собственно, именно этой возможностью и можно воспользоваться для вставки объекта в текстовый редактор.

1. Перейдите в меню «Файл» программы Компас, выберите «Сохранить как», а затем выберите подходящий тип файла (JPEG, BMP, PNG).

2. Откройте Ворд, кликните в том месте, куда нужно добавить объект, и вставьте изображение точно таким же образом, как это описано в предыдущем пункте.

Примечание: Данный метод тоже исключает возможность редактирования вставленного объекта. То есть, вы сможете изменить его, как и любой рисунок в Word, но не сможете редактировать, как фрагмент или чертеж в Компасе.

Вставка с возможностью редактирования

И все-таки существует метод, с помощью которого вы можете вставить фрагмент или чертеж из Компаса-3D в Ворд в том же виде, в каком он находиться в САПР-программе. Объект будет доступен для редактирования непосредственно в текстовом редакторе, точнее, он будет открываться в отдельном окне Компаса.

1. Сохраните объект в стандартном формате Компаса-3D.

2. Перейдите в Word, кликните в нужном месте страницы и переключитесь во вкладку «Вставка».

3. Нажмите на кнопку «Объект», расположенную на панели быстрого доступа. Выберите пункт «Создание из файла» и нажмите «Обзор».

4. Перейдите в папку, в которой находится созданный в Компасе фрагмент, и выберите его. Нажмите «ОК».

Компас-3D будет открыт в среде Ворда, так что при необходимости вы сможете отредактировать вставленный фрагмент, чертеж или деталь, не покидая текстовый редактор.

Урок: Как чертить в Компас-3D

На этом все, теперь вы знаете, как вставить фрагмент или любой другой объект из Компаса в Ворд. Продуктивной вам работы и результативного обучения.

Как работает графический калькулятор для графиков функций?

Онлайн сервис работает очень просто. В поле на самом верху вписывается функция (т.е. само уравнение, график которого необходимо построить). Сразу после ввода приложение моментально рисует график в области под этим полем. Все происходит без обновления страницы. Далее, можно внести различные цветовые настройки, а также скрыть/показать некоторые элементы графика функции. После этого, готовый график можно скачать, нажав на соответствующую кнопку в самом низу приложения. На ваш компьютер будет загружен рисунок в формате .png, который вы сможете распечатать или перенести в бумажную тетрадь.

Сжатие (растяжение) графика к (от) оси ординат.Симметричное отображение графика относительно оси

Первая группа действий связана с умножением АРГУМЕНТА функции на число. Для удобства я разобью правило на несколько пунктов:

Сжатие графика функции к оси ординат

Это случай когда АРГУМЕНТ функции умножен на число, бОльшее единицы.

Правило: чтобы построить график функции , где , нужно график функции  сжать к оси  в  раз.

И первой на эшафот взойдёт функция, которой я недавно грозился:

Пример 1

Построить график функции .

Сначала изобразим график синуса, его период равен :
К слову, чертить графики тригонометрических функций вручную – занятие кропотливое, поскольку  и т.д., то есть на стандартной клетчатой бумаге аккуратным нужно быть вплоть до миллиметра, даже до полумиллиметра. Впрочем, многие с этим уже столкнулись.

Теперь поиграем на бесконечно длинном баяне. Мысленно возьмём синусоиду в руки и сожмём её к оси  в 2 раза:
То есть, график функции  получается путём сжатия графика  к оси ординат в два раза. Логично, что период итоговой функции тоже уполовинился:

В целях самоконтроля можно взять 2-3 значения «икс» и устно либо на черновике выполнить подстановку:
Смотрим на чертёж, и видим, что это действительно так.

Аналогичную блиц-проверку полезно осуществлять в любом другом примере! Более того, она лучше поможет усвоить суть того или иного преобразования.

Пример 2

Построить график функции

«Чёрная гармошка»  сжимается к оси  в 3 раза:
Итоговый график  проведён красным цветом.
Исходный период  косинуса закономерно уменьшается в три раза:  (отграничен жёлтыми точками).

Растяжение графика функции от оси ординат

Это противоположное действие, теперь баян не сжимается, а растягивается.
Случай имеет место, когда АРГУМЕНТ функции умножается на число .

Правило: чтобы построить график функции , где , нужно график функции  растянуть от оси  в  раз.

Продолжим мучить синус:

Пример 3

Построить график функции

Берём в руки нашу «бесконечную гармошку»:

И растягиваем её от оси  в 2 раза:

То есть, график функции  получается путём растяжения графика  от оси ординат в два раза. Период итоговой функции увеличивается в 2 раза: , он толком даже не вместился на данный чертёж.

Операции сжатия/растяжения графиков, разумеется, выполнимы не только для тригонометрических функций:

Пример 4

Построить графики функций

График функции  получается путём сжатия графика экспоненты  к оси  в два раза. А график  – путём растяжения графика экспоненты  от оси  в два раза:

В качестве ассоциации можете опять поиграть на «баяне» .

Продолжаем систематизировать  умножение аргумента функции на число:
Мы рассмотрели два случая – сжатие () и растяжение ().

Очевидно, что нет практического смысла рассматривать значения . Есть более интересный вопрос: что происходит, когда аргумент умножается на отрицательное число? Ответ будет получен чуть позже, а пока рассмотрим распространённый частный случай, когда :

Симметричное отображение графика функции относительно оси ординат

АРГУМЕНТ функции меняет знак.

Правило: чтобы построить график функции , нужно график  отобразить симметрично относительно оси .

Наглядный пример уже встречался на уроке Графики и свойства элементарных функций (вспоминаем ). Распечатаем ещё один комплект:

Пример 5

Построить график функции

График функции  получается путём симметричного отображения графика  относительно оси ординат:

Как видите, всё просто.

Если при умножении аргумента на число  значение параметра  отрицательно и не равно минус единице, то построение выполняется в два шага. Например: . На первом шаге выполняем сжатие графика  к оси ординат в 2 раза: . На втором шаге график  отображаем симметрично относительно оси ординат: . Конкретный пример обязательно рассмотрим ниже.

А следующий параграф посвящается одному интересному человеку из дворовой компании моего далёкого детства. Он вытягивал руки в стороны, открывал рот и прыгал влево/вправо по проезжей части. Водители крутили виском у пальца, сигналили, но догнать его так никто и не смог.

Вариант 1: График функции X^2

В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.

1. Создайте строку X, где укажите необходимый диапазон чисел для графика функции.

Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.

Нажмите по первой ячейке и впишите , что значит автоматическое возведение указанной ячейки в квадрат.

Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.

Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».

На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».

В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».

Подойдет вариант «Точечная с гладкими кривыми и маркерами».

После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.

Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.

Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».

Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.

Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.

Графики тригонометрических функций

С чего начинаются тригонометрические мучения в школе? Правильно. С синуса

Построим график функции

Данная линия называется синусоидой.

Напоминаю, что «пи» – это иррациональное число: , и в тригонометрии от него в глазах рябит.

Основные свойства функции :

Данная функция является периодической с периодом . Что это значит? Посмотрим на отрезок . Слева и справа от него бесконечно повторяется точно такой же кусок графика.

Область определения: , то есть для любого значения «икс» существует значение синуса.

Область значений: . Функция  является ограниченной: , то есть, все «игреки» сидят строго в отрезке .
Такого не бывает:  или , точнее говоря, бывает, но указанные уравнения не имеют решения.

Синус – это функция нечетная, синусоида симметричная относительно начала координат, и справедлив следующий факт: . Таким образом, если в вычислениях встретится, например, , то минус терять здесь ни в коем случае нельзя! Он выносится:

Как ведет себя синус на бесконечности? Попробуем провести исследование с помощью пределов:,  Чему равны такие пределы? Запомните, данных пределов не существует. По вполне понятным причинам, график синуса болтается как как неприкаянный, то дойдет единицы, то уйдет к минус единице и так до бесконечности.

Вот вам пример, когда предела не существует. В высшей математике это можно встретить не очень часто, но такое понятие, как «предела не существует» – существует!

В практических вычислениях желательно (и даже обязательно) знать и помнить следующие значения синуса: , , . Другие значения синуса (а также остальных тригонометрических функций) можно найти в методическом материале Тригонометрические таблицы.

График косинуса

Построим график функции

График косинуса – это та же самая синусоида, сдвинутая вдоль оси  на  влево
(см. также Пример 8 урока о геометрических преобразованиях графиков).

Поэтому почти все свойства синуса справедливы и для косинуса. За некоторым, но существенным исключением.

Косинус – это функция четная, ее график симметричен относительно оси  , и справедлив следующий факт: . То есть, минус перед аргументом косинуса можно безболезненно убирать (или наоборот, ставить). В отличие от синуса в косинусе минус «бесследно пропадает».

Для решения практических задач нужно знать и помнить следующие значения косинуса: , , .

Графики тангенса и котангенса

Построим график функции

Основные свойства функции :

Данная функция является периодической с периодом . То есть, достаточно рассмотреть отрезок , слева и справа от него ситуация будет бесконечно повторяться.

Область определения:  – все действительные числа, кроме …  , , , … и т. д. или коротко: , где  – любое целое число. Множество целых чисел (… -4, -3, -2, -1, 0, 1, 2, 3, 4, …) в высшей математике обозначают жирной буквой Z.

Область значений: . Функция  не ограничена. В этом легко убедиться и аналитически: – если мы приближаемся по оси  к значению  справа, то ветка тангенса уходит на минус бесконечность, бесконечно близко приближаясь к своей асимптоте . – если мы приближаемся по оси  к значению  слева, то «игреки» шагают вверх на плюс бесконечность, а ветка тангенса бесконечно близко приближается к асимптоте .

Тангенс – функция нечетная, как и в случае с синусом, минус из-под тангенса не теряется, а выносится: .

В практических вычислениях полезно помнить следующие значения тангенса: , , , а также те точки, в которых тангенса не существует (см. график).

График котангенса – это почти тот же самый тангенс, функции связаны тригонометрическим соотношением . Вот его график:

Свойства попробуйте сформулировать самостоятельно, они практически такие же, как и у тангенса.

ChartGo

Англоязычный сервис для разработки многофункциональных и разноцветных гистограмм, линейных графиков, круговых диаграмм.

Для обучения пользователям представляется подробное руководство и деморолики.

ChartGo будет полезен для тех, кто нуждается в создании диаграмм регулярно. Среди подобных ресурсов отличается простотой «Create a graph online quickly».

Построение графиков онлайн осуществляется по таблице.

В начале работы необходимо выбрать одну из разновидностей диаграмм.

Приложение обеспечивает пользователям ряд простых вариантов настройки построения графиков различных функций в двумерных и трехмерных координатах.

Можно выбрать одну из разновидностей диаграмм и переключаться между 2D и 3D.

Настройки размера обеспечивают максимальный контроль между вертикальной и горизонтальной ориентацией.

Пользователи могут настраивать свои диаграммы с уникальным названием, а также присваивать названия для X и Y элементов.

Для построения графиков онлайн xyz в разделе «Example» доступно множество макетов, которые можно изменять на свое усмотрение.

Обратите внимание! В ChartGo в одной прямоугольной системе может быть построено множество графиков. При этом каждый график составлен с помощью точек и линий

Функции действительного переменного (аналитические) задаются пользователем в параметрическом виде.

Разработан и дополнительный функционал, который включает мониторинг и вывод координат на плоскости или в трехмерной системе, импорт и экспорт числовых данных в определенных форматах.

Программа имеет гибко настраиваемый интерфейс.

После создания диаграммы, пользователь может воспользоваться функцией печати результата и сохранения графика в виде статичного рисунка.

Читают сейчас

Оставить комментарий

Как рисовать в Ворде

1. Для начала работы следует перейти на вкладку «Вставка», где можно найти необходимые инструменты для рисования, а точнее фигуры, из которых и будет состоять будущее изображение.

Нажав на кнопку «Фигуры», пользователь получает доступ ко всем возможным фигурам для рисования.

Из предложенных программой можно выбрать одну подходящую и начать процесс рисования. Кликнув по пиктограмме нужной геометрической фигуры, можно перенести её на лист с помощью левой кнопки мышки.

Также можно создать полотно, где тоже можно рисовать. Его преимуществом является то, что текст будет находиться только за его границами.

1. Для того, чтобы создать новое полотно, перейдите на вкладку «Вставка» и нажав на кнопку «Фигуры», выберите опцию «Новое полотно».

Далее можно подстроить готовое полотно под себя (увеличить размер, изменить заливку и так далее).

Редактирование фигур

• Поворот
• Перемещение
• Изменение длинны, ширины или высоты объекта. Либо просто растяжение.

Для того, чтобы получившийся рисунок стал целым объектом, необходимо объединить все те фигуры, из которых собственно его и собрали.

1. Сначала для этого необходимо выделить поочерёдно каждый элемент левой кнопкой мыши, удерживая клавишу Ctrl.
2. Затем правой кнопкой мыши вызвать контекстное меню, в котором в пункте «Группировать»выбрать одноимённую опцию.

Изменение заливки фигур

По умолчанию, нарисованные фигуры имеют синий цвет заливки, поэтому при необходимости можно с лёгкостью заменить их цвет на подходящий.

Для начала следует двойным щелчком левой кнопки мыши выбрать рисунок, и в открывшейся сверху вкладке в пункте «Заливка» выбрать нужный цвет. Готово.

Изменение цвета контура рисунка

Это также несложная процедура, которая выполняется аналогично предыдущей. После того, как объект выбран, в пункте «Контур фигуры» выберите желаемый цвет. Также в этом же меню можно подобрать толщину контура.

Возможно и изменение линий, которыми будет обведено изображение.

Изменения стиля фигуры

1. Выбрав объект двойным нажатием ЛКМ, переходим на ту же самую вкладку, о которой было сказано в двух предыдущих пунктах.
2. Слева от пунктов «Заливка» и «Контур» видим палитру всех предложенных стандартной библиотекой Ворда стилей оформления фигуры. Далее выбираем подходящий и готово.

Добавление эффектов

Почему бы не добавить чего-нибудь специфического для украшения созданного рисунка? Например, свечение, тень, отражение и многие другие. В этом случае будет использовано специальное меню, где можно подобрать спецэффекты по вкусу. Можно также поэкспериментировать с расширенными настройками. Они находятся снизу каждой группы эффектов.

Передний и задний план

При создании рисунка фигуры накладываются друг на друга. Например, как на картинке ниже:

То есть, для того, чтобы полумесяц переместить за тучи, необходимо кликнуть по нему ПКМ и выбрать пункт «На задний план». В случае, если его придётся переместить обратно, можно воспользоваться опцией «На передний план».

Что делать, если при перемещении текста передвигается фигура?

Эту проблему очень легко устранить. Достаточно нажатия правой кнопкой мыши по созданному рисунку. В меню «Обтекание текстом» выбрать опцию «Зафиксировать положение на странице». Вуаля!

Расширенные опции форматирования изображений

Желаете отредактировать созданное изображение более детально? Воспользуйтесь меню «Формат фигуры», которое вызывается кликом правой кнопки мыши.

«Формат фигуры» состоит из трёх вкладок:

• Заливка и границы;
• Эффекты;
• Макет и свойства.

А теперь о каждой вкладке подробнее.

Заливка и границы

В этой вкладке можно изменять заливку рисунка и линии, из которых он состоит. Например, можно сделать узорную, текстурную либо любую другую заливку. Также можно изменить толщину линий и их прозрачность. К тому же, тут можно поэкспериментировать и с другими опциями.

Эффекты

Эта вкладка содержит в себе расширенные инструменты для подстройки спецэффектов. К примеру, здесь можно более точно отрегулировать прозрачность, размер, цвет. Также возможно добавить размытие и многие другие украшения.

Макет и свойства

Функции этой вкладки позволяют настроить положение текста, который обтекает рисунок, и позволяют установить размер полей в документе.

Рисование объёмных фигур

В Ворде возможно так же и создание трёхмерных изображений. Нарисовав обычную фигуру, перейдите в меню «Формат фигуры», где во вкладке «Эффекты» найдите подпункт «Формат объёмной фигуры». Затем внесите свои параметры.

Используя вышеприведённые инструкции, можно создать достаточно интересную композицию в Ворде. Надеемся, этот материал был для Вас полезным.

Масштабный сетевой график

1. Вычислить табличным методом все основные характеристики работ и событий, найти критический путь и его продолжительность.
2. Построить масштабный сетевой график.
3. Оценить вероятность выполнения всего комплекса работ за 30 дней.
4. Оценить максимально возможный срок выполнения всего комплекса работ с вероятностью 95%.

Код работы ( i,j)	Продолжительность
tmin (i,j)	tmax (i,j)
1,2	5	10
1,4	2	7
1,5	1	6
2,3	2	4,5
2,8	9	19
3,4	1	3,5
3,6	9	19
4,7	4	6,5
5,7	2	7
6,8	7	12
7,8	5	7,5

Решение находим с помощью сервиса Сетевая модель. В нашем задании продолжительность выполнения работы задаётся двумя оценками – минимальная и максимальная. Минимальная оценка характеризует продолжительность выполнения работы при наиболее благоприятных обстоятельствах, а максимальная t_max(i,j) – при наиболее неблагоприятных условиях. Продолжительность работы в этом случае рассматривается, как случайная величина, которая в результате реализации может принять любое значение в заданном интервале. Такие оценки называются вероятностными (случайными), и их ожидаемое значение t_ож(i,j) оценивается по формуле
t_ож(i,j)=(3 t_min(i,j)+2 t_max (i,j))/5
Для характеристики степени разброса возможных значений вокруг ожидаемого уровня используется показатель дисперсии:
S2(i,j)=0,04(t_max(i,j)-t_min(i,j))2Рассчитаем ожидаемое значение и показатель дисперсии.
t_ож(1,2)=(3*5+2*10)/5=7
t_ож(1,4)=(3*2+2*7)/5=4
t_ож(1,5)=(3*1+2*6)/5=3
t_ож(2,3)=(3*2+2*4,5)/5=3
t_ож(2,8)=(3*9+2*19)/5=13
t_ож(3,4)=(3*1+2*3,5)/5=2
t_ож(3,6)=(3*9+2*19)/5=13
t_ож(4,7)=(3*4+2*6,5)/5=5
t_ож(5,7)=(3*2+2*7)/5=4
t_ож(6,8)=(3*7+2*12)/5=9
t_ож(7,8)=(3*5+2*7,5)/5=6
S2(1,2)=0,04*(10-5)2=1
S2(1,4)=0,04*(7-2)2=1
S2(1,5)=0,04*(6-1)2=1
S2(2,3)=0,04*(4,5-1)2=0,25
S2(2,8)=0,04*(19-9)2=4
S2(3,4)=0,04*(3,5-1)2=6,25
S2(3,6)=0,04*(19-9)2=4
S2(4,7)=0,04*(6,5-4)2=0,25
S2(5,7)=0,04*(7-2)2=1
S2(6,8)=0,04*(12-7)2=1
S2(7,8)=0,04*(7,5-5)2=0,25

Полученные данные занесем в таблицу.

Таблица – Сетевая модель.

Работа ( i,j)	Продолжительность	Ожидаемая продолжительность tож(i,j)	Дисперсия S2(i,j)
tmin (i,j)	tmax (i,j)
1,2	5	10	7	1
1,4	2	7	4	1
1,5	1	6	3	1
2,3	2	4,5	3	0,25
2,8	9	19	13	4
3,4	1	3,5	2	6,25
3,6	9	19	13	4
4,7	4	6,5	5	0,25
5,7	2	7	4	1
6,8	7	12	9	1
7,8	5	7,5	6	0,25

КПР	Код работы (i,j)	Продолжительность работы t(i, j)	Ранние сроки	Поздние сроки	Резервы времени
tрн(i,j)	tро(i,j)	tпн(i,j)	tпо(i,j)	Rп	Rc
1	2	3	4	5	6	7	8	9
1,2	7	7	7
1,4	4	4	17	21	17	8
1,5	3	3	19	22	19
1	2,3	3	7	10	7	10
1	2,8	13	7	20	19	32	12	12
1	3,4	2	10	12	19	21	9
1	3,6	13	10	23	10	23
2	4,7	5	12	17	21	26	9
1	5,7	4	3	7	22	26	19	10
1	6,8	9	23	32	23	32
2	7,8	6	17	23	26	32	9	9

_кр

Рисунок — Масштабный график сетевой модели

P(t_кр
где Z=(Т-Т_кр)/S_крZ- нормативное отклонение случайной величины, S_кр – среднеквадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути.
Соответствие между Z и Ф(Z) представлено в таблице.

Таблица — Таблица стандартного нормального распределения.

Z	F(Z)	Z	F(Z)	Z	F(Z)
0.0000	1.0	0.6827	2.0	0.9643
0.1	0.0797	1.1	0.7287	2.1	0.9722
0.2	0.1585	1.2	0.7699	2.2	0.9786
0.3	0.2358	1.3	0.8064	2.3	0.9836
0.4	0.3108	1.4	0.8385	2.4	0.9876
0.5	0.3829	1.5	0.8664	2.5	0.9907
0.6	0.4515	1.6	0.8904	2.6	0.9931
0.7	0.5161	1.7	0.9104	2.7	0.9949
0.8	0.5763	1.8	0.9281	2.8	0.9963
0.9	0.6319	1.9	0.9545	2.9	0.9973

Критический путь проходит по работам (1,2)(2,3)(3,6)(3,8). 
Дисперсия критического пути:
S2­(L_кр)= S2(1,2)+ S2(2,3)+ S2(3,6)+S2(6,8)=1+0,25+4+1=6,25
S(L_кр)=2,5
p(t_кр<30)=0,5+0,5Ф((30-32)/2,5)=0,5-0,5Ф(0,8) = 0,5-0,5*0,5763=0,5-0,28815=0,213
Вероятность того, что весь комплекс работ будет выполнен не более чем за 30 дней, составляет 21,3%.
Для определения максимально возможного срока выполнения всего комплекса работ с надежностью 95% будем использовать следующую формулу:

T=Т_кр+Z*S_кр

Для решения поставленной задачи найдем значение аргумента Z, которое соответствует заданной вероятности 95% (значению графы Ф(Z)  0,9545*100% в таблице 5 соответствует Z=1,9).
T=32+1,9*2,5=36,8
Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95% составляет всего 36,8 дня.

Схема исследования поведения функций, применяемая для построения графиков функций

      Для построения   y = f (x)   желательно сначала провести исследование поведения функции   y = f (x)   по следующей схеме.

1. Найти   D ( f ).

2. Выяснить, является ли функция   y = f (x)   или

3. Выяснить, является ли функция   y = f (x)  

4. Найти асимптоты графика функции.

5. Вычислить производную функции   f ‘ (x) .

6. Найти функции   y = f (x) .

7. Найти интервалы и функции   y = f (x) .

8. Найти   y = f (x) .

9. Найти точки пересечения   y = f (x)   с .

   Если не удается точно найти нули функции, то есть точки, в которых график функции пересекает ось абсцисс   Ox,   то нужно попытаться найти интервалы, на которых нули функции располагаются. Часто эти интервалы удается найти, зная точки максимума и минимума функции.

10. Вычислить функции   f »  (x) .

11. Найти интервалы, на которых функция   y = f (x)   , а также интервалы, на которых функция   y = f (x)  .

12. Найти графика функции  y = f (x) .

      Замечание. Желательно рисовать схему поведения функции параллельно с проведением исследования свойств функции по описанному выше плану.