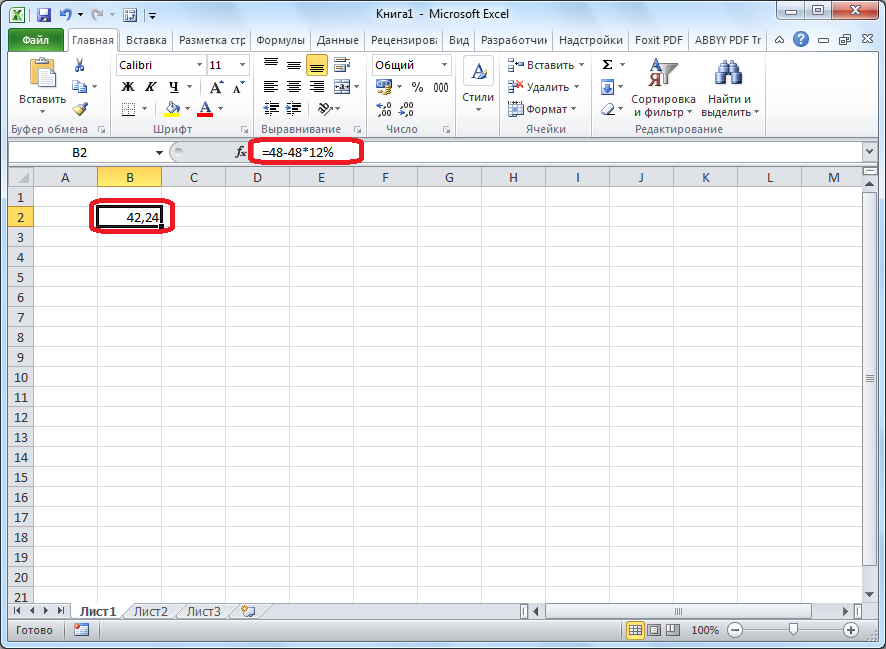
Как посчитать проценты: от числа, от суммы чисел и др. [в уме, на калькуляторе и с помощью excel]

Тарифы КликДенег

Как посчитать процент от числа

Лучше всего на этот вопрос ответить на конкретном примере. Давайте найдём 23 процента от числа 327. Для этого необходимо 327 умножить на 23 и результат поделить на 100. Получим:

(327 * 23) / 100 = 75,21

Получим ответ: 75,21

С точки зрения математики, данная задача сводится к пропорции (см. рисунок).

Как найти процент от числа на калькуляторе

Кнопка для вычисления процентов

Давайте научимся находить процент от числа с помощью калькулятора. Для начала убедитесь, что он способен это делать. Для этого найдите на его клавиатуре кнопку с изображением процента (%).

Найдём сколько составляют 17 процентов от числа 123.

1. вводим число 123 на калькуляторе;
2. нажимаем клавишу умножить (Х);
3. вводим 17;
4. нажимаем клавишу с изображением символа процента (%);
5. получаем на экране калькулятора ответ 20,91.

По аналогии можно найти любые другие проценты от любого числа.

Механизм работы

До сих пор мы рассматривали работу сложного процента в теории. Рассмотрим, что они из себя представляют на практике, на примере банковских депозитов и инвестиций.

На примере банковского депозита

При выборе банковского депозита вкладчик должен обращать внимание на несколько параметров: надежность банка, его участие в государственной системе страхования, условия пополнения и снятия денег, минимальная сумма на счете. Но главный из них – процентная ставка и условия ее начисления

Механизм сложных процентов подключен к вкладам с капитализацией процентов. А сама ставка, которая будет действовать на вашем счете, называется эффективной. Если вы не планируете снимать начисленный доход в течение всего срока накопления, то логично выбрать вклад именно с капитализацией.

Сравним полученный доход по депозиту с начислением процентов ежегодно, ежеквартально, ежемесячно и ежедневно. Первоначальные условия:

• сумма – 400 000 ₽;
• % ставка – 4 % годовых;
• срок вклада: 1, 2 и 3 года.

Сумма, которую получит вкладчик в конце срока, составит:

Срок депозита	Начисление процентов
1 раз в год	1 раз в квартал	1 раз в месяц	1 раз в день
1 год	416 000	416 241,6	416 296,62	416 323,38
2 года	432 640	433 142,68	433 257,18	433 312,9
3 года	449 945,6	450 730,01	450 908,75	450 995,73

В инвестициях

Сложный процент работает не только в банковской, но и в инвестиционной сфере. Если в банках процесс начисления процентов на проценты называют капитализацией, то в инвестициях – реинвестированием, т. е. повторным инвестированием. Но суть остается одинаковой.

Долгосрочные инвесторы хорошо знакомы с механизмом сложных % и стараются его использовать по максимуму. Рассмотрим, как он работает в различных инвестиционных инструментах.

Облигации

Доходность облигации складывается из двух источников – рост котировок и купоны. Последние выплачиваются в виде % от номинала ценной бумаги. Как правило, раз в полгода.

Эффект сложного процента можно наблюдать на купонных выплатах, но только в одном случае – если вы полученную прибыль не тратите на текущее потребление, а повторно вкладываете в инвестиции, т. е. реинвестируете. Понятно, что на доход от одной облигации мало что можно купить. Но если ценных бумаг несколько десятков или сотен, то сумма достаточна для покупки еще нескольких облигаций.

Из книги вы узнаете, как устроен мир прибыльного инвестирования

Скачать книгу

Например, владелец одной ОФЗ-26212-ПД 2 раза в год будет получать по 35,15 ₽. За год заработает 70,3 ₽. На эти деньги нельзя купить новую ОФЗ. Если облигаций не одна, а, например, 50 штук, то за год доход составит 3 515 ₽. Можно купить еще 3 ОФЗ за 1 085,81 ₽/шт. (котировка на 27.10.2020).

Если вы не держите облигацию до погашения, а пытаетесь заработать на росте котировок, то и в этом случае полученную прибыль от перепродажи лучше реинвестировать для включения механизма сложных %.

Акции

Точно такой же эффект, как описанный в предыдущем примере, может давать реинвестирование дохода от акций в покупку новых акций. Для этого полученные дивиденды не надо выводить со счета, а повторно инвестировать.

Не все эмитенты выплачивают дивиденды. Некоторые инвесторы покупают в свои инвестиционные портфели акции роста, т. е. бумаги, которые в перспективе могут вырасти в цене. Купил дешевле, продал дороже – одна из стратегий инвестирования. Сложный % заработает, если на полученную прибыль от перепродажи увеличится капитал в инвестициях, а не количество вещей в гардеробе.

Аналогично механизм “снежного кома” работает и с другими инструментами инвестиций. Эффект можно усилить, если инвестировать на ИИС, тогда каждый возврат подоходного налога (максимум 52 000 ₽ в год) необходимо опять возвращать на брокерский счет и покупать ценные бумаги.

Способ первый: процент от суммы через определение значения одного процента

Процент – одна сотая часть от числа и обозначается знаком %. Если разделить сумму на 100, то как раз получится один её процент. А дальше всё просто. Полученное число умножаем на нужное количество процентов. Таким способом легко посчитать прибыль по вкладу в банке.

Например, вы положили сумму в 30 000 под 9% годовых. Каким будет прибыток? Сумму 30 000 делим на 100. Получаем значение одного процента – 300. Умножаем 300 на 9 и получаем 2700 рублей – прибавку к первоначальной сумме. Если вклад — на два или три года, то этот показатель удваивается или утраивается. Бывают вклады, по которым выплату процентов производят ежемесячно. Тогда надо 2700 разделить на 12 месяцев. 225 рублей будут ежемесячным прибытком. Если проценты капитализируются (прибавляются к общему счёту), то каждый месяц сумма вклада будет увеличиваться. А значит, и процент будет высчитываться не от первоначального взноса, а от нового показателя. Поэтому в конце года вы получите прибыль уже не 2700 рублей, а больше. Сколько? Попробуйте посчитать.

Как на калькуляторе посчитать проценты

Лайфхак для подсчета процентов

Британец Бен Стефенс поделился в своем Twitter простым математическим трюком, существенно упрощающим подсчет процентов без калькулятора. Его можно сформулировать так: «А процентов от В — это то же самое, что В процентов от А».

Вроде бы ничего особенного, но в некоторых случаях помогает и еще как. Например, попробуй быстро посчитать сколько будет 16 % от 25. А 25 % от 16? И в том, и в другом случае ответ 4, но справиться со вторым примером, согласись, куда проще.

«Имею диплом математика и никогда об этом не задумывался», — пишут под твитом Бена одни пользователи. «Попробуй так найти 63 % от 11», — ехидничают другие. Что же, способ Бена действительно лучше работает с числами кратными 0 или 5. А 63 % от 11 будем находить по старинке.

Как вычислить процент от числа

Первый способ. Умножь процент и число друг на друга, а затем раздели на 100.
63 % от 11
63х11/100 = 693/100 = 6,93

Второй способ. Раздели число на 100 и умножь на процент.
63 % от 11
11/100 = 0,11 0,11х63 = 6,93

Кстати, легко умножать в уме любые двузначные числа на 11 мы научились в статье о приемах устного счета.

А если вместо 63 % от 11 найти 11 % от 63? На мой взгляд, лайфхак Бена вполне применим и здесь.
63 % от 11 — это то же, что и 11 % от 63
11 % = (10+1) %
63/10 = 6,3
63/100 = 0,63
6,3+0,63 = 6,93

Как узнать процент скидки

Пачка стирального порошка стоила в магазине 400 рублей. Сегодня в магазине скидки и на ценнике стоит 372 рубля. Как определить размер скидки в процентах?

Тут нужно составить пропорцию. Примем цену без скидки за 100 %, а цену со скидкой за х %. Тогда будет справедливым следующее равенство:
400/372 = 100/х
отсюда х = 372х100/400 = 93 %
Соответственно скидка составляет 7 %.

Узнаем процент с помощью калькулятора

Чтобы узнать процент от числа, введи число, знак умножения, затем нужный процент и знак %. Для задачи с порошком 7 % от 400 находим так: 400 × 7 %

Если нужно узнать цену после скидки, набери на калькуляторе: 400 — 7 %.

Небольшая подсказка: чтобы долго не искать калькулятор в меню смартфона, воспользуйся адресной строкой браузера (подойдет как «Яндекс», так и Google).

Как вычислить сложный процент с помощью онлайн-сервиса

Не все проценты можно посчитать, даже вооружившись нашей инструкцией.

Проценты по вкладам, доходность инвестиций, переплата по ипотеке — всё это проще вычислить, воспользовавшись удобными онлайн-сервисами.

Так, кредитный калькулятор в одно нажатие кнопки позволит рассчитать стоимость кредита, ежемесячные платежи погашения займа, полную сумму переплаты. А калькулятор сложных процентов поможет с начислением сложных процентов в банковском депозите (когда по окончании каждого периода начисленные проценты становятся основной суммой).

Яркие ценники, сигнализирующие о скидках, способны привлечь каждого. Но нужно быть бдительным. Ведь за пестрой россыпью процентов со знаком минус ушлые маркетологи иногда умудряются сбыть нам товар даже по более высоким ценам, чем до распродажи. А не попасться в их ловушки, сохранить деньги и сделать жизнь чуточку проще тебе, надеюсь, позволят наши полезные советы.

Формулы расчета

Раз есть сложный, значит, есть и простой процент. Несправедливо, если мы не разберем младшего брата нашего героя.

Простой процент

Простой процент каждый расчетный период (месяц, квартал, год) начисляется только на первоначальную сумму. Никакого эффекта “снежного кома” он не дает. Сумма увеличивается медленно.

Формула расчета:

S_N = S_П * (1 + % ст * N), где

• S_N – сумма в конце периода N;
• S_П – первоначальная сумма капитала;
• % ст – процентная ставка (доход);
• N – расчетный период.

Формула справедлива, если речь идет о начислении дохода раз в год. Например, положили на счет 100 000 ₽ под 10 % годовых на 10 лет. В конце срока получите: 100 000 * (1 + 0,1 * 10) = 200 000 ₽.

В реальной жизни понятие простого % применяется, например, в экономических расчетах по банковским вкладам без учета капитализации. В договоре обязательно указывается годовая процентная ставка. Проценты начисляются за каждый день нахождения денег на вкладе. А получать доход вкладчик может ежемесячно, ежеквартально или раз в год.

В этом случае формула примет вид:

S_N = S_П * (1 + % ст * Д / 365), где

Д – количество полных дней нахождения денег на депозите.

Например:

1. Положили на счет 100 000 ₽ под 10 % годовых на 91 день. В конце срока получите: 100 000 * (1 + 0,1 * 91 / 365) = 102 493,15 ₽.
2. На 180 дней: 100 000 * (1 + 0,1 * 180 / 365) = 104 931,51 ₽.
3. На 2 года (730 дней): 100 000 * (1 + 0,1 * 730 / 365) = 120 000 ₽.

Сложный процент с начислением дохода 1 раз в год

По методу сложных процентов при начислении дохода 1 раз в год будущая сумма определяется по формуле:

S_N = S_П * (1 + % ст)N

Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года. Будущая стоимость вклада составит: 100 000 * (1 + 0,1)2 = 121 000 ₽.

Сложный процент с начислением дохода чаще, чем 1 раз в год

Доход может начисляться ежемесячно, ежеквартально или 2 раза в год. Формула меняется:

S_N = S_N * (1 + % ст / К)N*К, где

К – частота начисления дохода (12, 4 или 2 раза в год).

Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года с ежемесячным начислением процентов. Будущая стоимость вклада составит: 100 000 * (1 + 0,1/12)24 = 122 039,1 ₽.

Как происходит начисление процентов на проценты?

Как известно, процент – это выплата определенной суммы денег, соразмерной вложенной или уставной сумме денег. Например, уставная сумма равна 1000 рублей, эта сумма положена под десять процентов. Десять процентов по-другому 0.1 от вложенной 1000 рублей. Перемножаем эти два числа и получаем сумму в 100 рублей, эта сумма и будет процентом по вкладу.

Данный метод называется методом простых процентов: мы просто взяли процент от числа и прибавили его к основному числу. Если анализировать данную теорию с математической точки зрения, то, принимая процент в долях за «x», а уставной капитал за «y», конечная сумма после процентного начисления «z» будет высчитываться по уравнению: z=y+y*x Таким образом, 1000+1000*0.1=1100.

Теперь разберем сложную систему начисления процентов. Допустим, денежная сумма была положена на определенный срок с условием, что по прошествии этого срока, клиент получит 10 процентов от суммы вклада, а по прошествии еще некоторого времени: 5% на сумму, уже выросшую в процентах.

Разберем эту ситуацию сначала просто на словах, а потом научимся записывать в уравнениях, чтобы вы могли при необходимости подставить любые цифры и высчитать прибыль. Итак, сначала по прошествии определенного срока на вклад будет начислен процент. Предположим, что вклад также равен 1000 рублей. Тогда 10 процентов от этого вклада, как мы уже писали выше, будет составлять 100 рублей. Когда закончится срок вложения, вкладчик будет иметь на своем счету 1100 рублей. Когда пройдет еще некоторое время, ему начислят 5 процентов на имеющуюся, то есть уже увеличенную сумму денег. Таким образом, несложно сделать подсчет: прибавляем пять процентов к имеющейся сумме в 1100 рублей, для этого умножаем 1100 на 0.05 и получаем в конечном результате сумму на вкладе в размере 1155 рублей.

Как записать этот расчет в виде уравнения, чтобы можно было подставлять в него любые другие цифры и считать без проблем? Для этого мы берем наше первичное уравнение z=y+y*x и меняем его. К полученной в уравнении первом прибыли мы должны взять еще некоторый процент (обозначим его как х1), после чего уравнение примет вид: z=(y+y*x)+(y+y*x)*х1.

Вспомните школьные годы, в математике обязательно были задачки на проценты, которые далеко не всем нравятся, потому что в них надо вникать.

Мы разобрали начисление процентов по сложной и простой схеме, теперь давайте узнаем, где используется сложная система процентов.

Зачем нужно уметь считать проценты?

В процессе пользования кредитной картой можно укладываться в льготный период и не платить процентов за использование кредитного лимита. Однако, не всегда этот маневр удается, и пользователю бывает сложно внести всю потраченную сумму вовремя.

Для этих случаев банки разрешают внести минимальный платеж, который состоит из части основной потраченной суммы, процентов, комиссий (СМС, страховка, стоимости обслуживания карты), штрафов и пеней (при наличии непогашенной задолженности за предыдущие периоды). Минимальный платеж нужно вносить обязательно в установленную дату.

Нужно примерно знать, какой минимальный платеж внести — чтоб подкопить денег и заплатить по карте вовремя. Это позволит не попасть на просрочку. Для банка оплата минимального платежа будет служить доказательством того, что клиент намерен погашать долг частями.

Meaning of control userpasswords2?

Эффективная процентная ставка по вкладу

Эта характеристика актуальна только для вкладов с капитализацией процентов. В связи с тем, что проценты не выплачиваются а идут на увеличение суммы вклада, очевидно, что если ежемесячно возрастает сумма вклада, то и вновь начисленные на эту сумму проценты также будут выше, как и конечный доход.

Если рассчитать, сколько процентов было начислено к начальной сумме к концу срока вклада, эта величина и будет являться эффективной процентной ставкой.

Формула расчета эффективной ставки:

где N — количество выплат процентов в течение срока вклада,T —  срок размещения вклада в месяцах.

Эта формула не универсальна. Она подходит только для вкладов с капитализацией 1 раз в месяц, период которых содержит целое количество месяцев. Для других вкладов (например вклад на 100 дней) эта формула работать не будет.

Однако есть и универсальная формула для рассчета эффективной ставки. Минус этой формулы в том, что получить результат можно только после рассчета процентов по вкладу.

Эта формула подходит для всех вкладов, с любыми сроками и любой периодичностью капитализации. Она просто считает отношение полученного дохода к начальной сумме вклада, приводя эту величину к годовым процентам. Лишь небольшая погрешность может присутствовать здесь, если период вклада или его часть выпала на високосный год.

Именно этот метод используется для рассчета эффективной ставки в представленном здесь депозитном калькуляторе.

Налог на доход по вкладам

Налоговый кодекс Российской Федерации предусматривает налогооблажение вкладов в следующих случаях:

• Если процентная ставка по рублевому вкладу превышает значение ключевой ставки ЦБ РФ на момент заключения или пролонгации договора, увеличенной на 5 процентных пунктов.
• Если процентная ставка по валютному вкладу превышает 9%.

Ставка налога составляет 35% для резидентов РФ и 30% для нерезидентов.

При этом налогом облагается не весь доход, полученный от вклада, а только часть, полученная в результате превышения процентной ставки по вкладу пороговой ставки. Для того, чтобы рассчитать налоговую базу (сумму, облагаемую налогом), нужно сначала рассчитать проценты налисленные по номинальной ставке вклада, а затем сделать аналогичный расчет по пороговой ставке. Разница этих сумм и будет являться налоговой базой. Для получения величины налога остается умножить эту сумму на ставку налога.

Наш депозитный калькулятор рассчитает ваш вклад с учетом налогов.

Definition and Usage

Как считать проценты при помощи калькулятора (на Айфоне, планшете и т.д.)

Считать в голове, конечно, очень полезно, однако порой гораздо удобнее достать смартфон и произвести все действия парой движений в приложении калькулятор. Например:

• Считаем скидку 4% от покупки смартфона стоимостью 25 000 рублей (находим процент от числа) — вводим 25 000 × 4, жмем знак «%» и «=», получаем 1000 рублей скидки;
• В примере с депозитом на 700 тысяч рублей под 20% годовых — вводим 700 000 × 20, жмем знак «%» и «=», получаем 140 000 рублей прибыли. Здесь же можно отметить, что если в выражении заменить «×» на «+», соответственно, 700 000 + 20 и нажать «%» и «=», то в ответе получим сразу сумму исходного числа (т.е. 700 000) + 20% (т.е. 140 000), то есть 840 000 рублей.

И так далее.

В наиболее сложных ситуациях на помощь придут специальные калькуляторы с готовыми формулами, которыми можно пользоваться онлайн. Например, на сайтах planetcalc.ru и allcalc.ru можно найти специальные программы для расчета кредитных и депозитных ставок, ипотек, субсидий и т.д.

Способ третий: считаем на калькуляторе

Если сомневаетесь в своих математических способностях, то воспользуйтесь калькулятором. С его помощью считается быстрее и точнее, особенно если речь идёт о больших суммах. Проще работать с калькулятором, у которого есть кнопка со знаком процент %. Сумму умножаем на количество процентов и нажимаем кнопку %. На экране высветится необходимый ответ.

Например, вы хотите посчитать, каким будет ваше пособие по уходу за ребёнком до 1,5 лет. Оно составляет 40% от среднего заработка за два последних закрытых календарных года. Допустим, средняя зарплата получилась 30 000 рублей. На калькуляторе 30 000 умножаем на 40 и нажимаем кнопку %. Клавишу = трогать не нужно. На экране высветится ответ 12 000. Это и будет величина пособия.

Как видите, всё очень просто. Тем более, что приложение «Калькулятор» сейчас есть в каждом сотовом телефоне. Если специальной кнопки % у аппарата нет, то воспользуйтесь одним из двух описанных выше способов. А умножение и деление произведите на калькуляторе, что облегчит и ускорит ваши вычисления.

Не забудьте: для облегчения подсчётов есть онлайн-калькуляторы. Действуют они так же, как и обычные, но всегда под рукой, когда вы работаете на компьютере.

Как использовать калькулятор процентов

Кроме обычного соотношения чисел и их процентного эквивалента, с помощью калькулятора можно провести простые математические вычисления увеличения или уменьшения заданного числа на количество процентов. Для этого достаточно заполнить соответствующие поля и нажать на кнопку “Рассчитать”.

Например, чтобы узнать сколько составит 5% от числа 80, ставим значения внужные поля. После нажатия кнопки расчета получим результат “4”.

Точно также калькулятор посчитает в каком процентном соотношении находятся два разных числа. Например 80 к 100 составит 80%.

С помощью калькулятора можно

• прибавить % — если к числу 80 прибавить 5%, то получим 84;
• вычесть % — если от числа 80 вычесть 5%, то получим 76.

Такие вычисления нужны, как для работы, так и в обычной жизни.

1. В магазине, когда мы видим на ценнике скидку 35%, калькулятор поможет быстро посчитать, какую сумму фактически надо заплатить.
2. На кухне, когда готовим блюдо, часто надо делать пересчет при изменении количества порций.
3. На работе, например в магазине, когда надо проанализировать соотношение выручки от нескольких продавцов, чтобы оценить качество работы. Также понадобится подсчет процентов для определения нагрузки, допустим почасовой, еженедельной и т.д.
4. Когда есть необходимость получения кредита. Вычисление суммы, которую включает процентная ставка, поможет подобрать наиболее выгодный вариант. То же касается и депозитов.
5. Не обойтись без процентов и копирайтерам. Любой заказчик хочет получить 100% уникальность при низком спаме и водности текста.

Как даже с 1 000 рублей в кармане создать пассивный доход к пенсии

Пенсионный возраст увеличили, накопительную пенсию заморозили, регулярно проводят пенсионную реформу и меняют условия. Все эти хаотичные телодвижения говорят только о том, что у руководства нет четкого плана действий и видения, как же должна начисляться пенсия в нашей стране.

Какой вывод простому гражданину нужно сделать из всего этого? Только один – накопить на пенсию самостоятельно. И поможет в этом сложный процент. На конкретных расчетах посмотрим, как даже с 1 000 ₽ в месяц создать пассивный доход. Но для начала замечательная сказка из книги Бодо Шефера “Мани, или Азбука денег”.

Жил-был когда-то крестьянин. Каждое утро он ходил в курятник, чтобы взять на завтрак яйцо, которое снесла его курица. Но однажды он нашел в гнезде не обычное яйцо, а золотое. Сначала он не мог в это поверить. Возможно, кто-то решил над ним зло подшутить. Но ювелир, которому он принес показать яйцо, подтвердил, что оно из чистого золота. Крестьянин выгодно продал яйцо и устроил большой праздник.

На следующее утро он пошел в курятник раньше, чем обычно. В гнезде опять лежало золотое яйцо. Так продолжалось несколько дней. Но крестьянин был жадным и хотел побыстрее разбогатеть. Он злился на свою курицу, потому что “глупая птица” не могла объяснить ему, как она умудряется нести золотые яйца. Ему казалось, что тогда он мог бы и сам нести золотые яйца. Тогда у него было бы каждый день по два яйца. И однажды крестьянин так сильно разозлился, что вбежал в курятник и зарезал свою курицу. Некому стало нести золотые яйца.

Мораль этой сказки такова: нельзя резать курицу, несущую золотые яйца. Но чтобы получать золотые яйца, надо сначала завести курочку. Этим вы и должны заняться как можно скорее. Время – друг инвестора и враг того, кто откладывает на потом создание личного капитала.

Пример 1. Необходимо рассчитать, сколько денег нужно накопить, чтобы жить на пассивный доход через какое-то количество лет. Допустим, мы хотим на пенсии ежемесячно получать 50 000 ₽. Учтем инфляцию 4 %.

Ставку доходности примем равной 10 %. Ее размер зависит от состава инвестпортфеля. Если решили копить в облигациях, то закладывать надо меньший %. Если составить сбалансированный портфель из разных инструментов (например, ETF, акции и облигации отдельных эмитентов, золото), то 10 % – очень консервативная оценка. На практике получается значительно больше.

Расчет без учета инфляции: 50 000 * 12 месяцев / 0,1 = 6 000 000 ₽. Для учета инфляции воспользуемся онлайн-калькулятором. Необходимо накопить уже 10 000 000 ₽.

Пример 2. Есть начальный капитал 50 000 ₽ с ежемесячным вложением равной суммы: 1 000 ₽, 5 000 ₽ и 10 000 ₽. Доходность – 10 %, примем ежегодное начисление %. Сколько накопим через 10, 20, 30 и 40 лет?

Сумма ежемесячных взносов	Срок накопления
10 лет	20 лет	30 лет	40 лет
1 000 ₽	320936,22	1023674,99	2846398,39	7574073,45
5 000 ₽	1085932,6	3772874,97	10742111,47	28818516,12
10 000 ₽	2042178,08	7209374,94	20611752,84	55374069,46

Какие выводы мы можем сделать из этих расчетов:

1. Накопить на пассивный доход в 50 000 ₽ в месяц мы сможем, откладывая 5 000 ₽ в течение 30 лет. Если инвестируем по 10 000 ₽, то уже примерно через 23 года можно выходить на пенсию.
2. С ежемесячными 1 000 ₽ нужно довольствоваться меньшей суммой пассивного дохода. Например, чтобы получать ежемесячно 35 000 ₽, надо накопить 7 000 000 ₽. Из таблицы видно, что только через 40 лет достигнем этого. А вот для ежемесячной прибавки к пенсии в 20 000 ₽ понадобится накопить 4 000 000 ₽ за 35 лет.

Поиграйте своими цифрами в любом финансовом калькуляторе сложных процентов. У кого-то начальная или ежемесячная сумма будет больше, кто-то рассмотрит меньший или больший срок и т. д.

Способ второй: переводим проценты в десятичную дробь

Как вы помните, процент — сотая часть числа. В виде десятичной дроби это 0,01 (ноль целых одна сотовая). Следовательно, 17% – это 0,17 (ноль целых, семнадцать сотых), 45% – 0,45 (ноль целых, сорок пять сотых) и т. д. Полученную десятичную дробь умножаем на сумму, процент от которой считаем. И находим искомый ответ.

Например, давайте рассчитаем сумму подоходного налога от зарплаты 35 000 рублей. Налог составляет 13%. В виде десятичной дроби это будет 0,13 (ноль целых, тринадцать сотых). Умножим сумму 35 000 на 0,13. Получится 4 550. Значит, после вычета подоходного налога вам будет перечислена зарплата 35 000 – 4 550 = 30 050. Иногда эту сумму уже без налога называют «зарплатой на руки» или «чистой». В противовес этому сумму вместе с налогом «грязной зарплатой». Именно «грязную зарплату» указывают в объявлениях о вакансиях компании и в трудовом договоре. На руки же даётся меньше. Сколько? Теперь вы легко посчитаете.

Нахождения числа по его проценту

Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

60 000 : 2 = 30 000

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

35 : 7 = 5

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

5 × 100 = 500

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

500 : 100 = 5

5 × 7 = 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

35 : 7 = 5

5 × 100 = 500

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

5 способов посчитать проценты от суммы с калькулятором и без

Простейшие формулы помогут узнать, выгодны ли скидки, и не нарушить пропорцию классного рецепта.

1. Как посчитать проценты, разделив число на 100

Так вы найдёте числовой эквивалент 1%. Дальше всё зависит от вашей цели. Чтобы посчитать проценты от суммы, умножьте их на размер 1%. Чтобы перевести число в проценты, разделите его на размер 1%.

Пример 1

Вы заходите в супермаркет и видите акцию на кофе. Его обычная цена — 458 рублей, сейчас действует скидка 7%. Но у вас есть карта магазина, и по ней пачка обойдётся в 417 рублей.

Чтобы понять, какой вариант выгоднее, надо перевести 7% в рубли.

Разделите 458 на 100. Для этого нужно просто сместить запятую, отделяющую целую часть числа от дробной, на две позиции влево. 1% равен 4,58 рубля.

Умножьте 4,58 на 7, и вы получите 32,06 рубля.

Теперь остаётся отнять от обычной цены 32,06 рубля. По акции кофе обойдётся в 425,94 рубля. Значит, выгоднее купить его по карте.

Пример 2

Вы видите, что игра в Steam стоит 1 000 рублей, хотя раньше продавалась за 1 500 рублей. Вам интересно, сколько процентов составила скидка.

Разделите 1 500 на 100. Сместив запятую на две позиции влево, вы получите 15. Это 1% от старой цены.

Теперь новую цену разделите на размер 1%. 1 000 / 15 = 66,6666%.

100% – 66,6666% = 33,3333%.Такую скидку предоставил магазин.

2. Как посчитать проценты, разделив число на 10

Этот способ похож на предыдущий, но считать с его помощью гораздо быстрее. Но только если речь идёт о процентах, кратных пяти.

Сначала вы находите размер 10%, а потом делите или умножаете его, чтобы получить нужное количество процентов.

Пример

Допустим, вы кладёте на депозит 530 тысяч рублей на 12 месяцев. Процентная ставка составляет 5%, капитализации не предусмотрено. Вы хотите узнать, сколько денег заберёте через год.

В первую очередь надо вычислить 10% от суммы. Разделите её на 10, передвинув запятую влево на один знак. Вы получите 53 тысячи.

Чтобы узнать, сколько составляют 5%, разделите результат на 2. Это 26,5 тысячи.

Если бы в примере речь шла о 30%, нужно было бы умножить 53 на 3. Для расчёта 25% пришлось бы умножить 53 на 2 и прибавить 26,5.

В любом случае такими крупными числами оперировать довольно просто.

3. Как посчитать проценты, составив пропорцию

Составлять пропорции — одно из наиболее полезных умений, которому вас научили в школе. С его помощью можно посчитать любые проценты. Выглядит пропорция так:

сумма, составляющая 100% : 100% = часть суммы : доля в процентном соотношении.

Или можно записать её так: a : b = c : d.

Обычно пропорция читается как «а относится к b так же, как с относится к d». Произведение крайних членов пропорции равно произведению её средних членов. Чтобы узнать неизвестное число из этого равенства, нужно решить простейшее уравнение.

4. Как посчитать проценты с помощью соотношений

В некоторых случаях можно воспользоваться простыми дробями. Например, 10% — это 1/10 числа. И чтобы узнать, сколько это будет в цифрах, достаточно разделить целое на 10.

• 20% — 1/5, то есть нужно делить число на 5;
• 25% — 1/4;
• 50% — 1/2;
• 12,5% — 1/8;
• 75% — это 3/4. Значит, придётся разделить число на 4 и умножить на 3.

5. Как посчитать проценты с помощью калькулятора

Если без калькулятора вам жизнь не мила, все вычисления можно делать с его помощью. А можно поступить ещё проще.

• Чтобы посчитать проценты от суммы, введите число, равное 100%, знак умножения, затем нужный процент и знак %. Для примера с кофе вычисления будут выглядеть так: 458 × 7%.
• Чтобы узнать сумму за вычетом процентов, введите число, равное 100%, минус, размер процентной доли и знак %: 458 – 7%.
• Аналогично можно складывать, как в примере с депозитом: 530 000 + 5%.